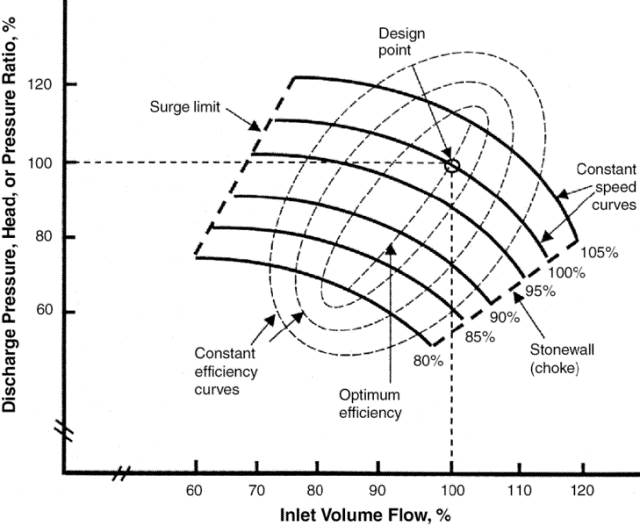
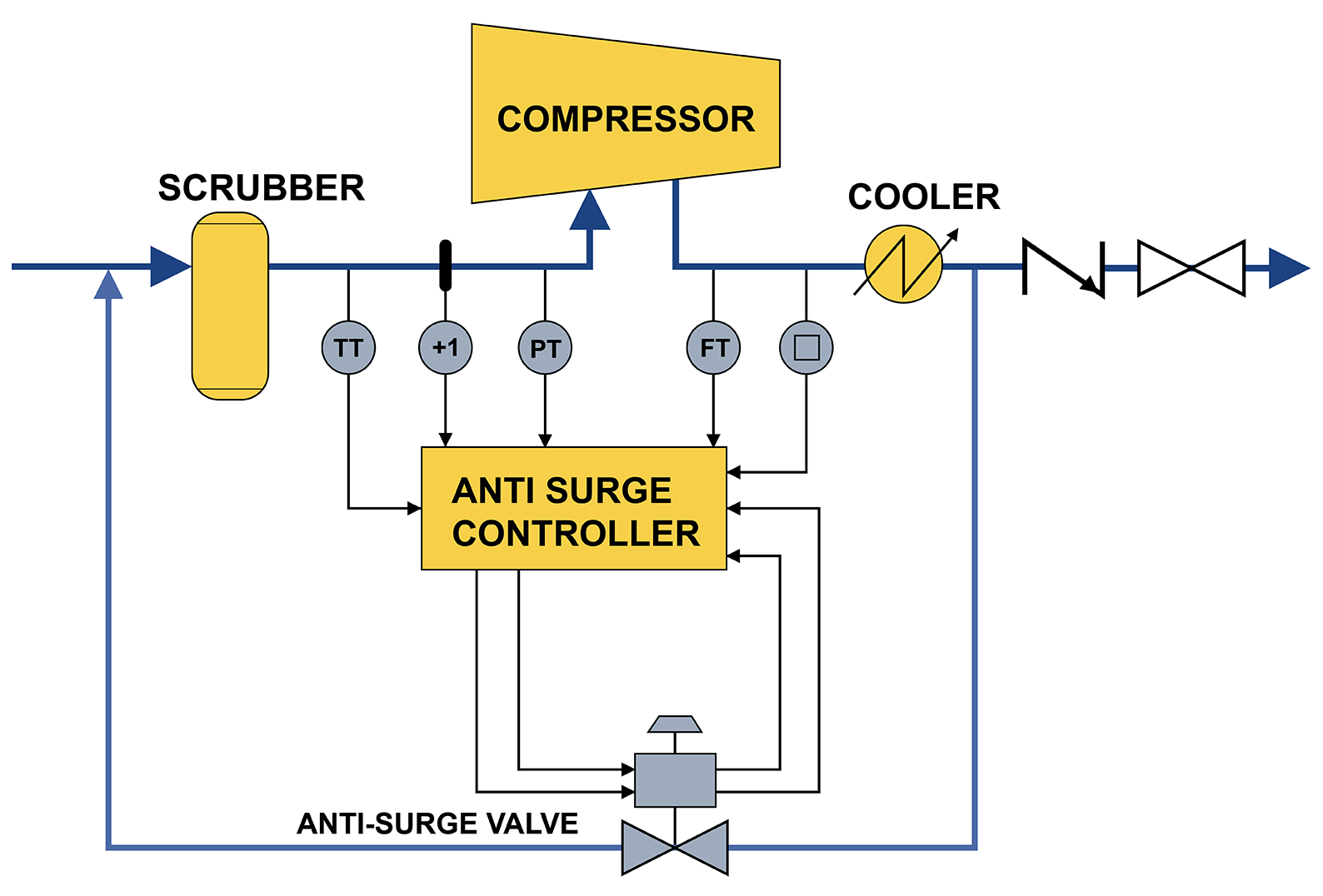
|
Hooman Fatoorehchi Assistant Professor School of Chemical Engineering University of Tehran, Tehran, Iran  Advanced Control Engineering Linear Quadratic Regular (LQR) [continuous form] Given the state equations of an LTI system as $\dot{x}= \bf{A}x + \bf{B}u$, we would like to find a control input $u$ such that it minimizes the cost function $J$: $J=\int_{t_0}^{t_1} \left( \bf{x^TQx+u^TRu} \right) dt$. The optimal control input would be: $\bf{u_{opt}}=-\bf{Kx}$, where $\bf{K}=\bf{R^{-1}B^TP}$, and $\bf{P}$ is obtained by solving the following matrix Riccati equations $\bf{\dot{P}=-PA-A^TP-Q+PBR^{-1}B^TP}$, with the following boundary condition: $\bf{x^T}(t_1)\bf{P}(t_1)\bf{x}(t_1)=\bf{0}$. Compressor Surge Control System: NOTE: Surging is not witnessed in reciprocating compressors. So, it concerns centrifugal and axial flow compressors.
|
