Hooman Fatoorehchi Assistant Professor School of Chemical Engineering University of Tehran, Tehran, Iran Formulas in this page are typed in $\LaTeX$. Root Locus Example 1) Sketch the root locus of the following control system: $ GH=K\frac{s^2-4s+20}{(s+2)(s+4)}$ . First, we calculate the zeros: $s^2-4s+20=0 \rightarrow z_{1,2}=\frac{4 \hspace{0.1cm}\pm \sqrt{(-4)^2-4(1)(20)} }{2} \rightarrow z_1= 2+4i, z_2= 2-4i.$ Secondly, we find the poles: $(s+2)(s+4)=0 \rightarrow p_1=-2, p_2=-4$ The number of the asymptotes is $ n-m = 2 - 2 = 0 $. The break-away and break-in points coordinates: $ \displaystyle \sum_{i=1}^{2} \frac{1}{s-p_i}=\sum_{i=1}^{2} \frac{1}{s-z_i} \rightarrow \frac{1}{s+2} + \frac{1}{s+4} = \frac{1}{s-2-4i} + \frac{1}{s-2+4i} \\ \rightarrow (s+4)(s-2-4i)(s-2+4i)+(s+2)(s-2-4i)(s-2+4i)=(s+4)(s+2)(s-2+4i)+(s+4)(s+2)(s-2-4i) \\ \rightarrow (s+4)((s-2)^2-(4i)^2)+(s+2)((s-2)^2-(4i)^2)=(s^2+6s+8)(s-2+4i)+(s^2+6s+8)(s-2-4i) \\ \rightarrow (s+4)(s^2-4s+20)+(s+2)(s^2-4s+20)=2(s^2+6s+8)(s-2) \\ \rightarrow (s^3+4s+80)+(s^3-2s^2+12s+40) = 2 (s^3+4s^2-4s-16) \\ \rightarrow 5s^2-12s-76 = 0 \rightarrow s_{1,2}=\frac{12 \hspace{0.1cm}\pm \sqrt{(-12)^2-4(5)(-76)} }{10}=\frac{12 \hspace{0.1cm}\pm \sqrt{1664} }{10} = 5.2792, -2.8792. $ To find the intersection of the root locus with the imaginary axis, we plug $s=ai$ into the characteristic equation: $ 1+K\frac{s^2-4s+20}{(s+2)(s+4)}=0$ $ 1+K\frac{(ai)^2-4ai+20}{(ai+2)(ai+4)}=0 \rightarrow (ai+2)(ai+4)+K ((ai)^2-4ai+20)=0 \rightarrow -a^2+6ai+8+K (-a^2-4ai+20)=0 \\ \rightarrow 8+20K-a^2(K+1) + (6a-4Ka)i =0 \\ \left\{ \begin{array}{lr} 6a-4Ka=0\\ 8+20K-a^2(K+1)=0 \end{array} \right. \Longrightarrow \left\{ \begin{array}{lr} 6-4K=0 \rightarrow K=1.5 \\ 8+20(1.5)-a^2(1.5+1)=0 \rightarrow a= \pm \sqrt{\frac{38}{2.5}}=\pm 3.8987 \end{array} \right. $ 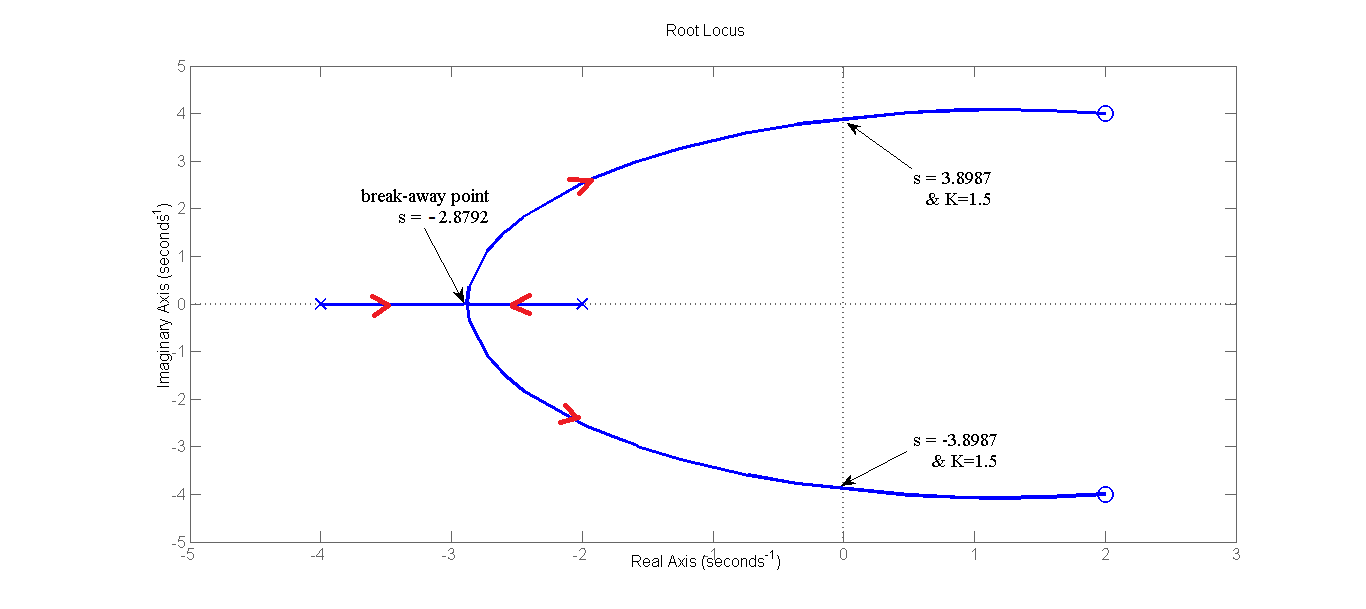% MATLAB code for Example 1 clc clear all close all h = tf([1 -4 20],[1 6 8]); rlocus(h) set(findall(gcf,'type','line'),'linewidth',2,'MarkerSize', 12); % The end Example 2) The open-loop transfer function of a system is given below. Sketch the root locus of the negative feedback control system: $ GH=K\frac{s+2}{(s+3)(s^2+2s+2)}$. Zeros: $z_1=-2$. Poles: $p_1=-3$, $p_{2,3}=\frac{-2 \hspace{0.1cm}\pm \sqrt{(2)^2-4(1)(2)} }{2} \rightarrow p_2= -1+i$, $p_3= -1-i$. Number of the asymptotes: $n-m = 3-1 = 2$. The aysmptotes' angles from the positive real axis: $ \theta_k = $ $\Large \frac{(2k+1)\pi}{n-m}$, $ k = 0, 1, \cdots, n-m-1 \rightarrow \theta_1=\frac{\pi}{2}, \theta_2=\frac{3\pi}{2}$. The intersection of the asymptotes on the real line $\Large \frac {\sum\nolimits_{i=1}^{n} p_i - \sum\nolimits_{i=1}^{m} z_i}{n-m}$ = $\frac{-3}{2}= -1.5$.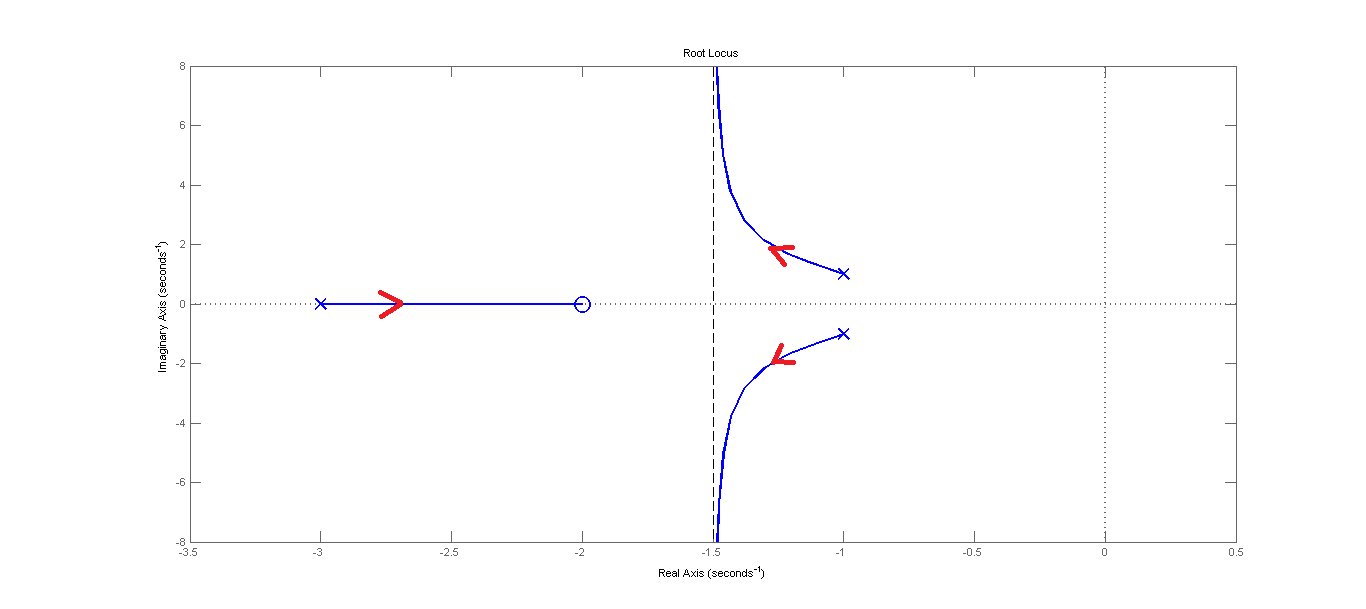